Как правильно определять углы

Шкалы транпортира

Транспортир KWB имеет две шкалы — основную и вспомогательную.

Шкалы хоть и нанесены краской, но считываются однозначно. Правда стойкость к износу у них ограничена.

У основной шкалы четыре ряда значений. Один нанесен сверху шкалы, три снизу — видны в смотровое окошко подвижной планки. Каждый ряд используется для своего метода измерения углов. Каждый метод опишем подробно ниже.

Цена делений основной шкалы — один градус.

Вспомогательная шкала на подвижной планке размечена под измерение долей градуса. Цена делений — 10′ (десять минут). То есть можно измерять углы с точностью до десяти минут или до 1/6 градуса (в десятичной системе).

Список источников

• yserogo.ru
• ru.wikihow.com
• interneturok.ru
• gvozdoder.com
• edufuture.biz
• urok.1sept.ru

Шаги

Метод 1

Измерение угла транспортиром

1. 1

   Оцените, к какому типу относится интересующий вас угол. Углы можно разделить на три класса: острые, тупые и прямые. Острые углы относительно узки (менее 90 градусов), тупые углы шире (более 90 градусов), а величина прямых углов составляет 90 градусов (их стороны перпендикулярны друг другу).

   На первый взгляд мы можем сказать, что выше изображен острый угол, то есть его величина меньше 90 градусов.

   Оцените на глаз, к какому типу принадлежит тот угол, который вы собираетесь измерить. Предварительная оценка поможет вам определить необходимый диапазон и правильно выбрать шкалу транспортира.

2. 2

   Приложите центр транспортира к вершине измеряемого угла. В середине транспортира есть небольшое отверстие. Приложите транспортир к углу так, чтобы это отверстие совпало с вершиной угла.

3. 3

   Поверните транспортир так, чтобы одна из сторон угла совпала с основанием инструмента. Не спеша поворачивайте транспортир и следите за тем, чтобы вершина угла оставалась в центре. В результате одна из сторон угла должна совместиться с основанием транспортира.

   При этом вторая сторона угла должна пересекать дугу транспортира (его округлую часть).

4. 4

   Проследите за второй стороной угла, которая пересекает дугу транспортира. Если вторая сторона не доходит до дуги инструмента, продлите ее. Можно также приложить к этой стороне угла лист бумаги, который доходил бы до дуги транспортира. Пересекаемое число покажет вам величину угла в градусах.

   • В приведенном выше примере величина угла составляет 70 градусов. При этом мы пользуемся меньшей шкалой, так как определили ранее, что имеем дело с острым углом, то есть его величина не превышает 90 градусов. Для тупых углов следует использовать более крупную шкалу со значениями больше 90 градусов.
   • На первых порах можно путаться со шкалой. Большинство транспортиров имеют две шкалы, одну на внутренней и вторую на внешней стороне округлой части. Это сделано для того, чтобы было удобно измерять углы как левой, так и правой ориентации.

Метод 2

Построение угла с помощью транспортира

1. 1

   Проведите прямую линию. Это будет опорная линия, которая послужит одной из двух сторон будущего угла. С ее помощью вы определите направление, в котором следует провести вторую сторону угла. Как правило, первую прямую линию удобно провести горизонтально.

   • При этом можно воспользоваться прямым краем транспортира.
   • Длина линии не важна.

2. 2

   Расположите центр транспортира на одном из концов проведенной линии. Это будет вершина будущего угла. Отметьте на бумаге точку вершины.

   Не обязательно располагать вершину на краю линии. Вершина угла может размещаться в любой точке на линии, просто удобнее использовать крайнюю точку.

3. 3

   Отыщите на соответствующей шкале транспортира необходимый вам угол. Приложите к прямой линии основание транспортира и отметьте на бумаге соответствующее число градусов. Если необходимо построить острый угол (менее 90 градусов), используйте шкалу с меньшими значениями. Для тупого угла воспользуйтесь шкалой с большими величинами.

   • Помните о том, что основание транспортира — это его прямая часть. Совместите его центр с вершиной будущего угла и отметьте на бумаге необходимую величину угла.
   • На приведенном выше видео величина угла составляет 36 градусов.

4. 4

   Проведите вторую сторону угла. С помощью линейки, прямого края транспортира или другого инструмента проведите вторую сторону угла — соедините вершину со сделанной ранее меткой. В результате у вас получится заданный угол. С помощью транспортира можно измерить угол и убедиться, что все правильно.

• карандаш или ручка
• бумага
• транспортир
• линейка (необязательно)

Измерение углов

Измерить угол — значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.

Обычно за единицу измерения углов принимают градус. Градус — это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак ° , который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).

Измерение углов транспортиром

Для измерения углов используют специальный прибор — транспортир:

У транспортира две шкалы — внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.

Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:

Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов и пишут: ∠BOC = 60°, ∠MON = 120°.

Для более точного измерения углов используют доли градуса: минуты и секунды. Минута — это угол, равный части градуса. Секунда — это угол, равный части минуты. Минуты обозначают знаком ‘ , a секунды — знаком ” . Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:

Свойства измерения углов

Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.

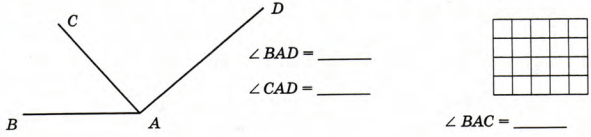
Рассмотрим угол AOB:

Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.

Развёрнутый угол равен 180°.

Любой угол имеет определённую величину, большую нуля.

История изобретения

Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.

Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников. Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.

Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.

Возможно, в то же время, учёные Индии также разработали тригонометрическую систему, основанную на функции синуса, которая, в отличие от используемого в настоящее время синуса, была не пропорцией, а длиной стороны, противоположной углу в прямом треугольнике этой гипотенузы. Индийские математики использовали разные значения для этого в своих таблицах.

Томас Бландевиль рассказал о приборе специально созданном, для рисования и измерения фигур в своём «Кратком описании универсальных карт» 1589 года. Как видно из названия, он применял его, чтобы править навигационные карты для использования в высоких широтах.

Другие европейские математики также описывали подобные приборы примерно в то же время. Независимо от того, кто первым придумал этот инструмент, к началу XVII века он вошёл в стандартную практику мореплавателей и геодезистов. К XVIII веку транспортиры начали появляться в учебниках по геодезии и геометрии.

В то время предпочтительными материалами для их изготовления были:

• дерево;
• латунь;
• серебро;
• медь;
• слоновая кость.

В первой половине XX века начали применять олово и целлулоид.

Называться транспортиром (рус.) прибор стал в 1610 году. Термин произошёл от средневекового слова protractor, что означает «переносить», который, в свою очередь, произошел от латинского слова protrahere «тянуть вперёд».

Определение угла

Определение 1

Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.

Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.

Определение 2

Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.

Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.

Перейдем к понятию определения угла.

Определение 3

Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.

Имеет место случай, когда стороны угла могут выступать в роли прямой линии.

Определение 4

Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.

На рисунке ниже изображен развернутый угол.

Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.

Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .

Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.

Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Внутренняя область угла – элемент, служащий для второго определения угла.

Определение 5

Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.

Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе “египетского треугольника”. Однако
это только в теории линии просто чертятся на бумаге, “ловить” же все выбранные размеры растянутыми шнурами или
линиями на полу – задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся
последовательность разметки изображена на картинках ниже

Важно не забывать: диагональ 141,4 см. нужно умножать на
количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах.
Картинки увеличиваются по клику!

Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах.
Картинки увеличиваются по клику!

Что называют поворотом точки вокруг точки?

Сразу отметим, что наряду с фразой «поворот вокруг точки» будем также использовать словосочетания «поворот около точки» и «поворот относительно точки», что обозначает одно и то же.

Введем понятие поворота точки вокруг точки.

Сначала дадим определение центра поворота.

Определение.

Точку, относительно которой осуществляется поворот, называют центром поворота.

Теперь скажем, что получается в результате поворота точки.

В результате поворота некоторой точки A относительно центра поворота O получается точка A₁ (которая в случае некоторого количества может совпадать с A), причем точка A₁ лежит на окружности с центром в точке O радиуса OA. Иными словами, при повороте относительно точки O точка A переходит в точку A₁, лежащую на окружности с центром в точке O радиуса OA.

Считают, что точка O при повороте вокруг самой себя переходит в саму себя. То есть, в результате поворота вокруг центра поворота O точка O переходит в саму себя.

Также стоит отметить, что поворот точки А вокруг точки O стоит рассматривать как перемещение в результате движения точки А по окружности с центром в точке O радиуса OA.

Для наглядности приведем иллюстрации поворота точки А вокруг точки O, на рисунках, расположенных ниже, перемещение точки А в точку А₁ покажем при помощи стрелки.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером
в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены —
это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих
стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно
больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250
см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат
(умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 —
это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра
должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали —
проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Длина a
Длина b Расчет
Диагональ c

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же,
не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое
нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из
понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров
не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены
на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Сравнение углов

Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:

\ и \ полностью совмещаются при наложении следовательно: \

\ и \ не совмещаются при наложении: \

Причем: \

При этом развернутые углы всегда являются равными.

Совмещение углов \ и \ происходит следующим образом:

1. Вершину B одного угла совмещаем с вершиной N другого угла.
2. Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.

Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.

Если нет, то один угол — меньше другого: ∠ABC<∠MNK.

Некоторые важные теоремы, основанные на прямых и углах:

1. Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
2. Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
3. Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
4. Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
5. Вертикальные углы равны, когда прямая пересекает прямые. Линии могут быть как параллельными, так и непараллельными.

Совет 2: Как сделать закругленные края

Методов и техник тонирования существует великое множество, но сегодня я познакомлю вас с такой техникой, которая, за счет использования режимов наложения слоев, максимально упрощает весь процесс.

Запрещено вносить изменения в графический материал, например, обрезание водяного знака или перекрытие его своим знаками. Форум для обсуждения качества перевода и интерфейса русской версии Фотошопа.

Далее, камера сама сшивает полученные кадры или это делает поставляемое с камерой ПО (как в моем случае с Olympus PEN E-PL1, камера помечала нужные снимки, а программа «ib» сама сшивала панораму). Но, даже тогда, я понимал что такой способ очень тугой. Тогда я предпочитал фотошоп.

Она экономит время, да и сшивает не хуже фотошопа (иногда и лучше). Кроме того, как и в фотошопе, в ней можно выбирать тип проекций, автоматическую или ручную обрезку, размер изображения и т.д. Ладно, с объяснениями в любви заканчиваю, перехожу к демонстрации.

Я снимал в режиме приоритета диафрагмы (Av). Параметры подбираешь по ситуации. Если в каком-то месте панорама сшилась не правильно (не совсем точно), можно изменить размер исходных снимков и панорама склеится по новому.

Чтобы это сделать, наведём курсор мыши на линейку, зажмём левую кнопку мыши и переместим курсор на картинку.. Проведём направляющую градиента от верхнего правого угла, к нижнему левому. Когда мне впервые было нужно закруглить углы в иллюстрации для сайта, ответ для меня был неочевиден.

Измеряем угол

Транспортир помогает построить и измерить угол. Градус — это общепринятая единица, которой пользуются для измерения углов. Встречается несколько разновидностей углов:

• Острый. Таким называют угол до 90 градусов.
• Прямым является угол, равный 90 градусам.
• Тупой угол варьируется в диапазоне от 90 до 180 градусов.
• Развёрнутый угол представляет собой прямую линию или 180 градусов.
• Полный угол выглядит как окружность и составляет 360 градусов.

Нетрудно разобраться, как измерить угол. Для того чтобы узнать, какова величина угла, нам необходимо установить транспортир таким образом, чтобы его центр располагался в вершине угла, а прямая сторона совпала с одной из его сторон. Шкала укажет нам количество градусов данного угла. Вот таким нехитрым способом мы можем узнать, что за угол перед нами.

Для построения угла с заданным градусом следует приложить прямую часть транспортира к линии, а его центр — к началу линии. Впоследствии эта точка будет являться вершиной угла. Затем на шкале отыскиваем заданное число и ставим точку. Теперь транспортир можно снять и соединить отрезком начало линии (вершину угла) с отмеченной точкой.

Школьные канцтовары, произведенные разными компаниями, отличаются по материалу, цвету, размеру. Так вот: тем, у кого транспортир оказался больше длины угла, и не представляется возможным определить его величину, сторону угла необходимо продлить, используя прямую линейку.

Информация о статье

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 25 человек(а).

Категории: Геометрия

На других языках:

English: Use a Protractor, Español: usar un transportador, Português: Usar um Transferidor, Italiano: Usare un Goniometro, Français: utiliser un rapporteur, 中文: 使用量角器, Bahasa Indonesia: Menggunakan Busur Derajat, Nederlands: Een gradenboog gebruiken, العربية: استخدام المنقلة

Эту страницу просматривали 159 017 раз.

Была ли эта статья полезной?

Да
Нет

Кликните на вкладку Paths. В правом верхнем углу найдите значок стрелки и кликните на него. В списке опций выберите «Make Selection…»

Rounded Rectangle в режиме Paths. Сделать обводку как надо, на вкладке Paths с контролом кликаем — получаем выделение. Если сохранять картинку в gif, то она теряет в качестве очень сильно (у меня, по крайней мере, так). Если в png-24, то начинает весить в 5 раз больше. Если вам нужно создать реалистичность и объемность фотографии, тогда вы зашли по адресу.

Выберите верхний слой там, где фотография и выполните следующие действия. Если вы являетесь пользователем социальных сетей, то наверняка замечали у многих друзей и знакомых симпатичные аватарки с закругленными углами. Сейчас у вас только один слой (Background), и он заблокирован. Затем создайте новый слой (Ctrl+Shift+N), поместите его между задним фоном и его копией как это показано на скриншоте (можно залить его каким-нибудь цветом, например белым).

Затем на фотографии выделите фрагмент, который вы хотите использовать (например, в качестве аватарки). Готово, вы получили слой с фотографией с закругленными углами. Фотографии с закругленными краями отлично дополняют дизайн сайтов, плакатов, аватарок и буклетов. В графическом редакторе Photoshop не существует встроенной опции или плагина для решения данной задачи. Запустите Photoshop и откройте фотографию, которую хотите закруглить.

В новом слое нарисуйте прямоугольник с закругленными краями с помощью инструмента Rounded rectangle tool . Цвет заливки не имеет значения. В списке слоев дважды кликните на новом слое, где только что нарисовали прямоугольник. Откроется окно настроек стиля слоя. В настройках Advanced Blending поставьте значение Fill Opacity на 0 (полностью прозрачное). В меню настройки «Make Selection…» убедитесь, что значение Feather Radius равно 0 пикселей.

Откройте ее в фотошопе и взгляните на окошко со слоями (на скриншоте слева внизу). Открываем новое окно в Фотошопе (Ctrl+N) и вставляем в него скопированный рисунок (Ctrl+V). Для новичков в этом уроке фотошопа я разложу все по полочкам, что куда нажимать. Нажимаем на клавиатуре M и кликаем в любом месте на холсте рисунка, чтобы снять выделение на готовом изображении аватарки с закругленными углами.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна
квадрату длины гипотенузы. В виде формулы записывается это так:

a²+b²=c²

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза.
Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем
размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник»

Это треугольник со сторонами 3, 4 и 5,
причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов

Проверим
данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все
сходится!

А теперь применим теорему на практике.

Как поставить знак градуса в Word

Если вы работаете с текстом в Word для вставки градуса можно использовать встроенную таблицу символов. Чтобы воспользоваться этим способом перейдите на вкладку « Вставка », нажмите на кнопку « Символ » и в открывшемся меню выберите вариант « Другие символы ».

В результате откроется окно с таблицей символов. Здесь нужно выбрать шрифт, с которым вы работает, а также набор символов « Дополнительная латиница-1 ». После этого нужно найти знак градуса в таблице и нажать на кнопку « Вставить ».

В результате выбранный символ будет вставлен в документ Word в том месте, где стоял курсор.

В дальнейшем знак градуса можно будет вставлять прямо из меню « Символ » на вкладке « Вставка », не открывая полную таблицу символов.

Также в Word можно знак градуса можно вставить с помощью надстрочного символа. Этот способ очень быстрый, но его можно считать неправильным, поскольку вставляется не сам знак градуса, а буква « о ».

Чтобы воспользоваться этим способом наберите нужное вам число и в конце добавьте букву « о ». После этого выделите эту букву и нажмите на кнопку « Надстрочный символ » на вкладке « Главная ».

В результате буква « о » превратится в некоторое подобие знака градуса.

Фокусировка и фокусное расстояние

Приведённая выше формула углового поля предполагает, что объектив сфокусирован на бесконечность. Лишь в этом случае эффективное фокусное расстояние объектива соответствует номинальному. При фокусировке объектива на более близких объектах эффективное фокусное расстояние может изменяться в определённых пределах, что влечёт за собой пропорциональное изменение угла обзора. В большинстве случаев плавание фокусного расстояния весьма незначительно и им можно смело пренебречь, однако при макросъёмке, когда расстояние до объекта сопоставимо с фокусным расстоянием объектива, эффект изменения угла обзора может стать вполне очевидным.

В идеале нам следовало бы подставлять в формулу значение именно эффективного фокусного расстояния для каждой конкретной дистанции фокусировки, но, к сожалению, это не всегда возможно.

Расчёт эффективного фокусного расстояния объектива сравнительно прост и прямолинеен только для классических фиксов, фокусировка которых осуществляется посредством выдвижения вперёд всего оптического блока. Иными словами, их эффективное фокусное расстояние увеличивается по мере увеличения масштаба съёмки, а угол обзора соответственно уменьшается. Эффективное фокусное расстояние в данном случае можно найти по формуле:

, где

F – эффективное фокусное расстояние;

f – номинальное фокусное расстояние;

R – дистанция фокусировки.

Впрочем, для большинства современных объективов эта формула практически бесполезна, поскольку при внутренней фокусировке эффективное фокусное расстояние может меняться самым неожиданным образом. Обычно объектив стараются проектировать так, чтобы по возможности свести к минимуму эффект изменения угла обзора при наводке на резкость. Так, многие современные объективы сохраняют угол обзора практически неизменным вне зависимости от дистанции фокусировки. Некоторые зумы имеют парадоксальную тенденцию к незначительному увеличению угла обзора на малых фокусировочных дистанциях. То есть по сравнению с традиционными объективами они ведут себя достаточно противоестественно.

Впрочем, повторюсь: при съёмке с нормальных дистанций всем этим колебаниям не стоит придавать слишком большого значения.

Видеоинструкция

На компьютерах под ОС Линукс необходимо ввести Composeoo, либо Shift+Ctrl+U и далее, после U, надо добавить b0↵ Enter. В системе вёрстки LaTeX применяйте команды \degree или \textdegree, которые соответственно расположены в пакетах gensymb или textcomp. В математическом режиме вызов знака (°) осуществляется комбинацией ^\circ.

Обозначение знака градуса (°) проставляется сразу после числового показателя. Не разделяется с цифровым значком пробелом. Связанные символы — Цельсий, С и Фаренгейт, F отделяются от знака (°) двумя типографскими пунктами, что, при текстовом наборе на ПК соответствует одному пробелу.

Отрицательное или положительное значение величины обозначается знаком +/- перед цифрой. Положительное/отрицательное положение показателя относительно нуля следует указывать для температурных данных.

Как определить крепость настойки в домашних условиях

Домашние алкогольные настойки — это отдельная категория напитков и снадобий. У многих народов можно найти свои, традиционные рецепты, о многих из них ходят легенды (наверняка все слышали о настойке “Зубровка”, например). Бывают также лекарственные рецепты домашних настоек, продукт которых употребляется покапельно и излечивает от самых разных недугов.

Для приготовления домашнего напитка требуется водка или самогон определенной крепости (зависит от рецепта). Однако в процессе настаивания градус напитка меняется (как правило, снижается). Поэтому возникает вопрос, как измерить крепость настойки, чтобы понимать, стоит ли ее корректировать.

Кстати, не бойтесь использовать самогон для рецептов настоек, если он приготовлен с соблюдением всех технологий. Например, аппарат Luxstahl 7m позволяет получать дистиллят и ректификат высокого качества, что при использовании добротного сырья окажется значительно лучше рядовой магазинной водки.

Как определить крепость настойки

Крепость — параметр физический. Он отражает процентное содержание этилового спирта в растворе. Поэтому определить такую цифру “на глаз” не получится. Без помощи инструментов можно лишь оценить, пройден ли порог в 40 градусов. Делается это так: наливаете настойку в ложку и поджигаете жидкость. Она будет гореть, если концентрация спирта в ней выше 40%. Если ниже — пламени в ложке не будет. Для определения точной цифры понадобится инструмент — ареометр (виномер, сахаромер, спиртометр). Это прибор для измерения плотности жидкости, градуированный таким образом, что шкала сразу показывает содержание этанола в растворе.

Как измерить крепость настойки спиртометром

Как правило, приборы для измерения крепости показывают наиболее точный результат при нормальном атмосферном давлении и температуре жидкости около 20°С. Для проведения измерений берется узкий высокий сосуд (лучше всего подходит мензурка, но можно взять высокий стакан, банку — все зависит от объема жидкости). Спиртометр опускается в жидкость плавно, чтобы избежать резкого удара об дно и повреждения инструмента (а все ареометры выполняются из стекла!). Спиртометр не должен касаться стенок емкости. Определяют значение содержания этанола по нижнему или верхнему мениску жидкости (указано в инструкции к прибору). Таким образом можно измерить крепость сладкой, горькой и любой другой настойки быстро и точно.

Можно ли измерить крепость настойки спиртометром-виномером?

Инструмент такого типа имеет достаточно узкий диапазон измерений (не выше 20% крепости), поэтому он пригоден лишь для измерения крепости браги, но не готового продукта.

Как сделать настойку крепче

Если полученные значения крепости не удовлетворили Вас, то можно укрепить настойку, добавив к ней порцию водки/самогона/спирта. Для достижения определенных значений крепости добавлять чистый продукт лучше не на глаз, а по формуле.

Например, у Вас имеется настойка крепостью 38 градусов, и Вы хотите довести ее до 40 градусов. Если у Вас имеется самогон с содержанием спирта 70%, то расчеты будут следующие:

Таким образом, нужно взять 30 частей раствора с концентрацией 38% и добавить к нему 2 части раствора с концентрацией 70% (т.е., например, к 300 мл настойки добавить 20 мл самогона)

Определение угла в математике

Определение

Что такое угол? Угол это — геометрическая фигура, образованная двумя лучами или линиями, имеющими общую конечную точку (вершину). Два луча называются сторонами угла, а точка, в которой пересекаются лучи, называется вершиной.

Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными.

Стороны угла – лучи, которые образуют угол (А, В).

Вершина угла – точка, из которой выходят лучи (О).

Угол делит плоскость на две части. Если угол не развернутый, то одна часть плоскости называется областью внутреннего угла, а другая часть называется областью внешнего угла. Ниже приведена картинка, поясняющая, какие части являются внешними, а какие внутренними.

Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.

• Положительный угол: если угол идет против часовой стрелки, то он называется положительным углом.
• Отрицательный угол: если угол направлен по часовой стрелке, то он называется отрицательным углом.

Интересно

Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб».

Понятие угла впервые использовал Евдем, который определил угол как отклонение от прямой линии.

Как обозначить углы?

Фигура угол отмечается символом «∠». Есть два разных способа обозначения углов:

• Способ 1: Как правило, угол обозначается строчными буквами, такими как «а», «х» и т. д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д.
• Способ 2:Используя три буквы на фигурах. Средняя буква должна быть вершиной (фактический угол).Например, ABC — треугольник. Чтобы представить угол A равным 60 градусам, мы можем определить его как ∠BAC = 60 °.

Типы углов

Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла.
Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.

1. Острый угол – это угол, градусная мера которого больше 0° и меньше 90°.
2. Прямой угол — когда измерение угла равно 90 градусов, он известен как прямой угол.
   Прямой угол можно легко наблюдать, так как он образует форму буквы L.
3. Тупой угол — когда измерение угла меньше 180 градусов, но больше 90 градусов,
   это тупой угол.
4. Развернутый угол — угол, образованный прямой линией, называется прямым углом. Это
   половина полного оборота круга. Размер прямого угла равен 180°.
5. Выпуклый угол – это угол, величина которого больше 180°, но меньше 360°.
6. Полный угол — когда измерение угла равно 360 градусам, это полный угол.

Ряд углов образуется при пересечении секущей двух или более прямых. Конкретные названия даны паре углов, что зависит от расположения угла по отношению к прямым. Линии могут быть как параллельными, так и непараллельными.